Успехът на Google се дължи предимно на създадения от тях алгоритъм за класиране, който успява бързо да покаже в SERP най-подходящите уеб страници за търсенето на потребителя. Всяка година Google променя своя алгоритъм за търсене около 500-600 пъти[1]. Тези актуализации влияят върху резултатите от търсенето и следователно върху приходите на индустрията и следователно трябва да се следят внимателно от специалистите. Повечето от тези промени са незначителни, но има няколко основни актуализации, които задължително трябва да се познават.
Page Rank
PageRank ( PR ) е първият и най-известен алгоритъм за измерване на относителното значение на уеб страниците в Мрежата и класирането им в резултатите от търсене на Google Search. Той е кръстен на Larry Page, един от основателите на Google.
Първата научна статия за Page Rank е публикувана през 1998 г. именно от Larry Page и Sergey Brin в резултат от работата им по изследователски проект на Стандфордския университет за нов вид търсачка[1].
PageRank работи, като оценява количеството и качеството на входящите хипервръзки, сочещи към дадена страница. Всяка хипервръзка към дадена страница се счита за глас на подкрепа и предава определена числова тежест. Основното предположение е, че по-важните уебсайтове вероятно ще получат повече връзки от други уебсайтове[2].
Резултатът от Page Rank се образува от математически алгоритъм, основан на уеб графиката, създадена от всички страници в Интернет. На всеки срещнат от ботовете елемент „Е“ в Мрежата се преписва числена тежест и се нарича “PageRank на E“. Той се определя рекурсивно и зависи от броя и PageRank показателите на всички страници, които се свързват с нея (входящите хипервръзки). Други фактори, като Author Rank и Trust Rank също допринесат за повишаване тежестта на елемента.
Чисто математически Page Rank извежда разпределение на вероятностите, използвано за изчисляване на вероятността даден човек, който случайно клика върху връзки, да отвори определена уеб страница.
В няколко научни източници се приема, че в първоначалната версия на алгоритъма сумата от Page Rank е равномерно разпределена между всички страници в мрежата по това време, а в по-късните версии разпределението на вероятностите се приема в цифрова стойност между 0 и 1. Стойност от 0.5 се приема като “50% вероятност” нещо да се случи. Следователно, Page Rank 0.5 означава, че има 50% вероятност човек, който кликне върху произволна хипервръзка, да бъде насочен към документ с причислен ранг равен на 0,5.
Нека разгледаме един опростен алгоритъм. Да приемем че имаме малка мрежа от четири страници: A, B, C и D (показани на фиг.3). Собствените връзки на страницата към самата нея или множество изходящи връзки от една страница към друга страница се игнорират. От тук ако приемем, че началната стойност е 1 следва, че всяка една от посочените в примера страници ще бъде равна на 0.25. Ако единствените връзки в системата бяха от страници B, C и D до A, всяка връзка ще прехвърли по 0.25 Page Rank на A при следващата итерация, за получен общ PR на страница А равен на 0.75.
PR(A) = PR(B)+ PR(C)+ PR(D) (1)
където PR(А) е PageRank на страница А;
PR(B), PR(C) и PR(D) са съответно ранговете на страници B, C и D.
Да предположим, че страница В има
връзка към страници С и А, страница C има само една връзка към страница А, а
страница D има връзки към всичките три страници, както е показано на фиг.3.
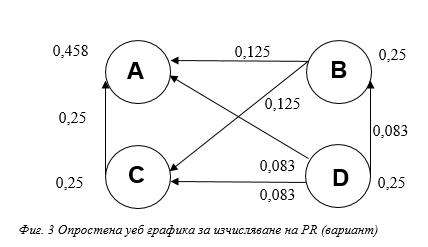
Тогава при първата итерация, страница B ще прехвърли половината от съществуващата първоначална стойност 0,25 на своя Page Rank, или по 0,125 на всяка от посочена страница С и А.
От своя страна страница C ще прехвърли цялата си тежест от 0,25 до единствената страница А към която води. Тъй като D има три изходящи връзки, то би прехвърлило по една трета от съществуващата си стойност или приблизително 0,083 към всяка една от тях.
Така ако сумираме всичко прехвърлено на страница А, то тя ще получи PageRank = 0.458.
Ситуацията на фиг. 3 за страница А математически следва да се изпише така:
С други думи предоставения Page Rank от дадена външна хипервръзка е равен на собствения рейтинг на документа, разделен на броя на изходящите му връзки L (pj).

където PR(А, B, C, D) е PageRank на съответната страница А, B, C, D;
L(B,C,D) e броя на изходящите връзки на всяка една страница B, C, D;
L (pj) – броя на изходящите връзки на страница pj.
На практика обаче всеки въображаем посетител, който случайно кликва върху група от хипервръзки, в крайна сметка ще спре да го прави.
Ако дадена страница няма връзки към други страници, тя прекъсва веригата на случайно сърфиране и принуждава посетителя да избере друг URL адрес с друга конфигурация на връзките.
Вероятността, на която и да е стъпка, че лицето ще продължи да разглежда колекцията се нарича коефициент на затихване – d.
Различни проучвания предлагат различни коефициенти на затихване, но най-често се приема да бъде 0,85[1].
Той се извежда от пълната вероятност 1, но при някои варианти на алгоритъма се дели на броя на документите ( N ) в колекцията[2].
При
всички случай обаче този коефициент се добавя към сумата от входящи връзки и
коригира PageRank на долу[3].
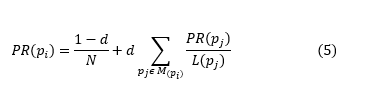
където p1, p2…..,pj са разглежданите страници в колекцията;
pi e дадената страница към която сочи съвкупността от връзки на останалите страници pj;
L – броя на изходящите хипервръзки на страниците pj;
d – коефициент на затихване;
N – общия брой страници в колекцията;
M(pi) е съвкупността от страници, към които се свързва pi.
В реалния свят броя на страниците в мрежата (N) е много голям, вероятността 1 / N е изключително малка, а с увеличението на страниците и коефициента d се променя във времето. Поради динамиката Google постоянно преизчислява резултатите от PageRank в мрежата и попълва своя Индекс. При всеки цикъл на преизчисляване страниците преразпределят текущия си PageRank. При итеративното изчисляване се използва доминиращ собствен вектор на стохастична матрица.
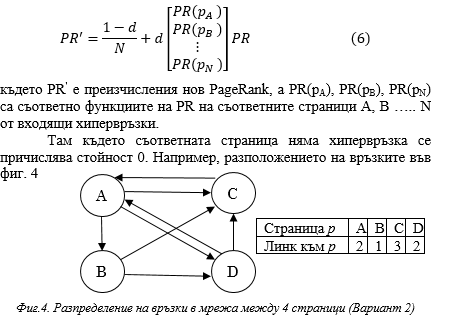
В таблицата до графиката са показани колко хипервръзки сочат към съответната страница. В следствие на тях страниците от посочения пример получават следните рангове:

Можем да забележим, че елементите на всяка колона се сумират до 1, така че това е стохастична матрица. По този начин тя може да се използва за измерване на собствени вектори и мрежов анализ. Стойностите на вектора PageRank могат да бъдат приближени до висока степен на точност само в рамките на няколко повторения.
Авторите на Google съобщават, че алгоритъм PageRank за мрежа, състояща се от 322 милиона връзки се доближава до допустима граница в 52 повторения[1].
От тези данни те заключават, че алгоритъмът може да бъде мащабиран много добре и факторът на мащабиране за изключително големи мрежи ще бъде линеен log N, където N е размерът на мрежата.
Точно на този принцип бе създадена груба модификация на алгоритъма наречена Google Toolbar PR с която потребителите можеха да видят приблизителния PageRank на страниците в Интернет. Тази възможност се предоставяше доскоро в лентата с инструменти на браузера. Там ранга се визуализираше с цяло число между 0 и 10, което нараства по логаритмична скала.
През март 2016 г. Google обявиха, че вече няма да поддържат тази възможност[2]. Въпреки, че прекратиха използването на Toolbar PR, Google все още използват резултатите от PageRank, когато определят как да класират съдържанието в резултатите от търсенето, но допълнително ги модифицират с различни актуализации.
Известни са много приложения на PageRank алгоритъм в редица други търсачки за класиране на академични и докторски програми, опити за заместване на импакт фактор и дори класиране на пътнико потока на летища и градски транспорт.
В началото на 2005 г. Google въведе нова стойност “nofollow” за атрибута rel на HTML хипервръзки, които разработчиците на уебсайтове да могат да поставят с цел да не се индексират определени линкове от Google за нуждите на PageRank.
Един от основните недостатъци на PageRank е, че не оценява добре новите страници. Дори и да са много качествени, те няма да имат много връзки, освен ако не са част от съществуващ сайт, като например Wikipedia.
В специализираните източници са предложени няколко стратегии за ускоряване на изчисляването на PageRank и подобряване резултатите от търсене, тъй като се появяват различни техники за манипулиране на резултатите и осигуряване на приходи от рекламни връзки.
В следствие на това той беше подобрен от алгоритмите
Trust Rank, Hummingbird, Rank Brain и други за които ще намерете информация
по-долу.
[1] Page, Lawrence; Brin, Sergey; Motwani, Rajeev; Winograd, Terry The PageRank citation ranking: Bringing order to the Web. http://ilpubs.stanford.edu:8090 /422/1/1999-66.pdf 1999
[2] Schwartz, Barry Google has confirmed it is removing Toolbar PageRank, 2018
[1] Brin, S.; Page, L. “The anatomy of a large-scale hypertextual Web search engine” Computer Networks and ISDN Systems. 30: 107–117. doi:10.1016/S0169-7552(98)00110-X. ISSN 0169-7552. 1998
[2] Matt Cutts, Straight from Google: What You Need to Know Archived. 2010
[3] Langville, Amy N.; Meyer, Carl D. Google’s PageRank and Beyond: The Science of Search Engine Rankings. Princeton University Press. 2006
[1] Page, Larry. PageRank: Bringing Order to the Web. // Stanford Digital Library Project, talk, August 18, 1997.
[2] Brin, S.; Page, L. (1998). “The anatomy of a large-scale hypertextual Web search engine”. Computer Networks and ISDN Systems. 30: 107–117. doi:10.1016/S0169-7552(98)00110-X. ISSN 0169-7552.
[1] DiSilvestro, A. 2017. Forcasting for the Future: How to Tract Google Algorithm Updates. Ac-cessed March 3 2017. https://www.searchenginejournal.com/forecasting-for-the-future-how-to-track-google-algorithm-updates/182208/